Integration by Parts How to Choose U and Dv

First choose which functions for u and v. Integration By Parts Formula.

Picking U And Dv For Integration By Parts Explained With Examples Youtube

Between x 2 and e x the factor e x is more sophisticated and you can integrate it so let d v e x d x and then u x 2.

. Filling in the box. I used to tell my students to set u equal to the part youd rather differentiate and dv equal to the part youd rather integrate. You remember integration by parts.

In other words we want to pick some ux and vx so that. If u and v are functions of x the product rule for differentiation that we met earlier gives us. LIPET is a tool that can help us in this endeavor.

The arrows in this figure remind you to differentiate on the left and to integrate on the right. U d v uv - v d u. Uv udvdxdx vdudxdx.

Sometimes integration by parts must be repeated to obtain an answer. Now that we have all the variables lets plug them into the integration by parts equation. Find du by taking the derivative of the u you chose in Step 1.

So lets do a couple of substitutions. We review their content and use your feedback to keep the quality high. Choose as d v the most complicated expression in the integrand that you currently know how to integrate.

V ⅓x 3. V du In applying integration by parts to a specific integral one pair of choices for u and dv may work while another pair may not. U x 1.

In your own words describe how to choose u and dv when using integration by parts. Let u x then du dx. Who are the experts.

This is not the easiest formula to use however. If u and v are any two differentiable functions of a single variable x. We may be able to integrate such products by using Integration by Parts.

This problem has been solved. The integral on the right can be expanded via a clever integration by parts. These are supposed to be memory devices to help you choose your u and dv in an integration by parts question.

Justify your answers with a thorough explanation of the mathematical concepts involved. X2 sin x dx u x2 Algebraic Function dv sin x dx Trig Function du 2x dx v sin x dx cosx x2 sin x dx uvvdu x2 cosx cosx 2x dx x2 cosx2 x cosx dx Second application of integration by parts. Set u to the first term you see.

Then well use that information to determine du and v. In fact if we choose u we know what dv must be in order to satisfy the equation above. Ddxuv udvdx vdudx By integrating both the sides we get.

An antiderivative of v is t but any function of the form t C will be another antiderivative. Make sure you also write the dx after the. Compute the integral of the following functions.

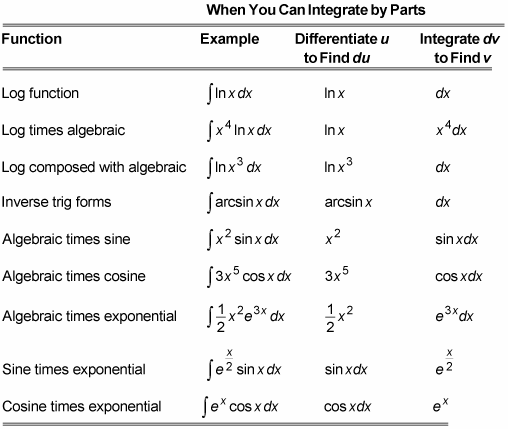
You also asked about integrating x ln. - Would you answer these - What is the product rule in integral form. L logarithmic I inverse trigonometric A algebraic T trigonometric.

The formula for this method is. Draw an empty 2-by-2 box then put your u ln x in the upper-left corner and your dv in the lower-right corner as in the following figure. - words explain the purpose of using a.

This is the part thats left. Udvdxddxuv-vdudx Integrating throughout with respect to x we obtain the formula for integration by parts. V dx cosx dx sinx see Integration Rules Now we can put it together.

Let u f x then du f x dx. Let us apply this theorem to find the integrals of functions in the given examples. Experts are tested by Chegg as specialists in their subject area.

U fx v gx du f xdx dv g xdx. For example you asked about integrating x 2 e x. V du in applying integration by parts to a specific.

The answer is. OK we have x multiplied by cosx so integration by parts is a good choice. V cosx So now it is in the format u v dx we can proceed.

The derivative of lnx is 1x dx and the antiderivative of x 2 is ⅓x 3. Integration by Parts - How to Choose u and dv Integrate p5 lnp dp Jakes Math LessonsIve been talking about integration methods like integration by. Thats not bad advice but it begs the question How do I know what I want to differentiate and what I want to integrate Until you have some experience and intuition thats hard to answer.

Ddxuvudvdxvdudx Rearranging we have. Using the LIATE mnemonic for choosing u and dv in integration by parts. The function which comes first in the series is to be picked as u and the other one as v.

U f x v g x d u f x d x d v g x d x. Let v g x then dv g x dx. Let dv sin xdx then v cos x.

To find the area of the shaded region we have to use integration by parts. For this integral lets choose utan1x and dvdx thereby making dudfrac1x21dx and vx. Take u t f t and v t 1.

Integration by Parts. Udvdxdx uv-vdudxdx1 Now let us consider. Explain how this rule is related to integration by parts.

When applying the formula for integration by parts how do you choose the u and dv. As noted above in the general steps you want to pick the function where the derivative is easier to. Both of these are just the standard Calculus I substitutions that hopefully you.

Many calc books mention the LIATE ILATE or DETAIL rule of thumb here. See the answer See the answer done loading. We try to see our integrand as and then we have.

The formula for Integration by Parts is then. To use integration by parts we want to make this integral the integral on the right-hand side of the fundamental equation. After applying the integration-by-parts formula Equation refIBP we obtain.

F x f a a x f t d t f x f a a x f t d t. Heres a good rule of thumb. For example for the integration of xsin x x is to be chosen as u as it comes first in.

This formula shows which part of the integrand to set equal to u and which part to set equal to d v. U x Algebraic function Making same choices for u and dv dv cosx Trig function. We can use the following notation to make the formula easier to remember.

Again first well choose a u and a dv. Then by the product rule of differentiation we have. And knowing dv tells us what vx is except for any constant.

U lnx dv x 2. Recall the method of integration by parts.

Integration By Parts How To Choose U Youtube

Integration By Parts

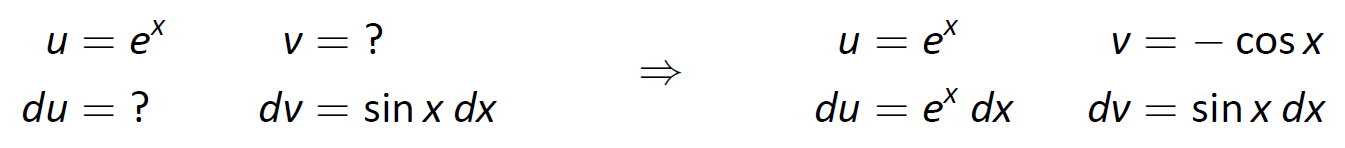
2 1 Integration By Parts Mathematics Libretexts

Calculus Integration By Parts Solutions Examples Videos

7 1 Integration By Parts Ppt Download

Integration By Parts Integration By Parts Calculus Ap Calculus

What Is An Easy Way To Choose U And Dv For Integration By Parts Quora

Ppt 6 2 Integration By Parts Powerpoint Presentation Free Download Id 5167805

Centers Of Mass Review Integration By Parts Center Of Mass 2 Dimensional Case The System S Center Of Mass Is Defined To Be Ppt Download

Solved Evaluate The Integral In X Dx X2 Step 1 2 In X To Chegg Com

Integration By Parts Ppt Download

Integration By Parts

What Is An Easy Way To Choose U And Dv For Integration By Parts Quora

Knowing When To Integrate By Parts Dummies

Calculus Integration By Parts Solutions Examples Videos

5044 Integration By Parts Ap Calculus Integration By Parts Product Rules For Integration A Is It A Function Times Its Derivative U Du B Is It A Ppt Download

Solved Evaluate The Integral In X Dx X2 Step 1 2 In X To Chegg Com

Picking U And Dv For Integration By Parts Explained With Examples Youtube

How To Do Integration By Parts More Than Once Dummies